Listado de la etiqueta: Matemáticas

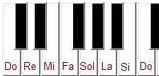
Hablando de escalas musicales, ¿qué os parece si hablamos también de escalas matemáticas? Venga, vamos a intentarlo. Respecto a lo primero, creo que está claro para todos nosotros: la escala musical más popular entre nosotros, la que actualmente más conocemos y usamos, está basada en siete notas, con los siguientes nombres: DO, RE, MI, FA, SOL, LA, SI. Fue el monje benedictino Guido D’Arezzo quien, a principios del siglo XI, puso nombre a las primeras seis primeras notas teniendo en cuenta las dos iniciales de un himno litúrgico dedicado a San Juan Bautista. Respecto a la séptima nota, SI, fue llamada de este modo por Anselmo de Flandes en el siglo XVI, en honor a San Juan: “Sancte Ioannes”. La acepción DO para la primera nota, que todos conocemos, fue hecha en el siglo XVII por Giovanni Battista Doni, que renombró así a la primera nota UT debido a su mejor adaptación al canto.

Bueno, pues la verdad es que esta escala con siete notas está muy bien, y es mundialmente conocida, pero existen otras escalas. Por ejemplo, podemos hablar de las escalas pentatónicas, con cinco notas musicales, y con diferentes esquemas de tonos y semitonos. Por ejemplo, podemos generar una escala pentatónica mayor teniendo en cuenta las teclas negras del teclado de un piano: do re mi sol la. Este tipo de escalas son muy comunes en China.

Otro ejemplo puede ser dado desde una escala pentatónica menor, que vendría dada por una escala muy relacionada con la música blues, y que genera multitud de canciones fácilmente identificables por los niños: la do re mi sol. Este escala es bastante conocida en la música andina.

Bien, ahora hablaremos de las escalas matemáticas. Concretamente, de las escalas logarítmicas. ¿Sabéis qué es un logaritmo? ¿No? Bueno, empecemos hablando de los números y del cálculo de las potencias de un número. A ver, si tenemos el número 2, y lo multiplicamos por él mismo, obtenemos el número 2×2=4. Y si lo multiplicamos por él mismo 3 veces, obtenemos 2x2x2=8. Naturalmente, esto lo podemos hacer tantas veces como queramos, por ejemplo, 8 veces: 2x2x2x2x2x2x2x2=256. Para simplificar la visualización de esta operación, las matemáticas utilizan la expresión 28=256, que se lee como “2 elevado a 8 es igual a 256”, o “2 a la 8ª potencia es igual 256”, o lo que es lo mismo: “256 es la 8ª potencia de 2”. De esta manera, en la expresión 28 se distingue el número denominado base, el 2, y el número llamado exponente, el 8.

Muy bien, pues si ahora entendemos esto, ¿podremos hacer el proceso inverso? Es decir, ¿podremos encontrar un número tal que 2 elevado a dicho número sea 256? O dicho de otro modo: ¿cuál es la potencia que hay que aplicar al número 2 para que se obtenga el número 256? Muy bien, pues este concepto es el de logaritmo: ¿cuál es el logaritmo del número 256 para la base 2? Pues el número 8, como hemos visto arriba. Expresándolo de otra manera, nos preguntaríamos ¿cuál es el exponente que hay que aplicar sobre la base 2 para obtener que su potencia es 256? ¡El 8! Estupendo, y ¿cómo expresamos matemáticamente esta operación? Pues del siguiente modo: log2256=8, que se lee como “el logaritmo en base 2 de 256 es igual a 8”, y que significa 28=256. Como podéis intuir, el cálculo del logaritmo y de la potencia son procesos inversos.

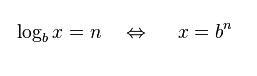
Quizás os estéis preguntando ahora por la utilidad de dichos conceptos. Bien, es natural, vamos a verlo. Venga, aquí va un ejemplo: ¿Cuál es la distancia media entre el planeta Tierra y el Sol? Mucha ¿verdad? Tratemos de expresarla en metros: Ciento cuarenta y nueve mil quinientos noventa y siete millones ochocientos setenta mil setecientos metros. ¿Qué número más grande, verdad? ¿Podremos expresarlo de otra manera más corta? Sí, con un número natural: 149.597.870.700m. Pero, ¿podemos simplicarlo todavía más? Sí, mediante una potencia: aproximadamente 1,5×1011m., es decir, 1,5 por 10 elevado a 11 metros. ¿Interesante, verdad? Hemos conseguido simplificar una cantidad enorme mediante solamente la expresión ‘1,5x1011m’. Pues ahora pensad en otras distancias mucho más lejanas, más allá de la Tierra y el Sol, como, por ejemplo, la distancia entre Neptuno y el Sol, a más de 4,5 billones de metros: gracias al uso de potencias podremos visualizar dichas distancias de un modo mucho más comprensible y sencillo. Así, si la Tierra estaba a 1,5x1011m, Neptuno está a 4,5x1012m. ¿Verdad que esta expresión es más simple que decir que están a 4.500.000.000.000m, esto es, a 4 billones 500 mil millones de metros?

En la tabla siguiente podemos ver esta simplificación de cantidades de una manera muy sencilla:

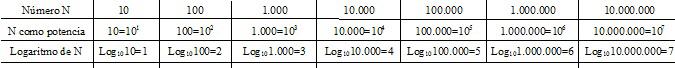
Muy bien, pues este invento es muy importante para obtener una representación más sencilla de los fenómenos físicos… hecho que nos conecta con la música: concretamente, con la representación de los sonidos. Como sábeis, el sonido es la propagación, a través del aire -y hasta nuestros oídos, si queremos oírlos-, de una presión, generalmente originada por la aplicación de una fuerza sobre una superficie, hecho que provoca su vibración. Esta vibración proviene de la caña de un clarinete, de los labios sobre la boquilla de un trombón, de la piel de un tambor, o de las cuerdas de un violín, por ejemplo.

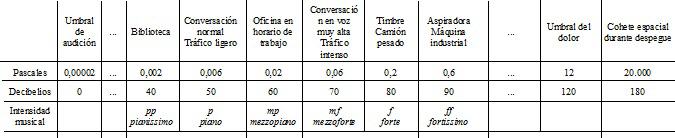
Muy bien, ya estamos llegando al final de nuestro viaje. A ver, esta presión que llega hasta nuestros oídos se mide en una unidad física que se denomina “pascal (Pa)”, y que equivale a la fuerza necesaria para proporcionar una aceleración de 1 m/s2 a un objeto de 1 kg de masa, y todo ello sobre una superficie de 1 metro cuadrado perpendicular a dicha fuerza. Pues bien, el oído humano es capaz de percibir sonidos entre 0.00002 Pa, umbral de audición, y unos 100 Pa, el umbral del dolor. De este modo, podemos oír desde el sonido de unas hojas mecidas por la brisa cuando vamos al campo, hasta el ruido producido por una excavadora o por la erupción de un volcán. Y, por supuesto, podemos oír música.

Estupendo, la cuestión es que si representásemos todos los sonidos posibles como pascales, pues tendríamos unas cantidades difíciles de visualizar: desde la cantidad 0.00002 Pa hasta la cantidad 100 Pa, que es 5 millones más grande, puesto que 0.00002 x 5.000.000 = 100. Y es por ello que se utiliza una escala logarítmica para simplicar esta visualización. Esta escala permite representar los sonidos mediante logaritmos, y no a través de pascales: permite traducir la escala de 5 millones de saltos, para pascales desde un mínimo de volumen hasta un máximo de volumen, a otra escala mucho más sencilla de entender y manejar. ¿Cómo podemos hacer esto? Pues mediante los decibelos (dB).

Decibelios… seguro que esta palabra os suena bastante más que la palabra logaritmo, ¿no? Pues vamos a ver brevemente que son conceptos similares. De hecho, al utilizar decibelios, estáis aplicando logaritmos. ¿Cómo? En la tabla siguiente podéis ver cómo se transforma una cantidad en otra: por ejemplo, cómo 0,006 pascales (el volumen de una conversación normal) se puede visualizar como 50 dB, que es una cantidad mucho más sencilla de entender. Y así con el resto de presiones expresadas en pascales. De este modo, y tal y como podéis apreciar en la última fila final de la tabla, la intensidad musical (el volumen, la presión en el aire de las vibraciones sonoras) puede expresarse mediante nuestras conocidas palabras italianas pianissimo o forte, o bien a través de los logaritmos ímplicitamente considerados en los decibelios: 50dB o 80dB.

Bueno, acabamos ya. Espero que el viaje desde las escalas musicales hasta las escalas logarítimas, visitando planetas a ritmo de blues, haya resultado interesante. Ya sabéis: si un día escucháis a vuestro director decir: “Por favor… más piano… más piano”, contestadle en escala logarítmica: “Muy bien… lo haremos casi a 50… casi a 50”.

¡Un fuerte abrazo para todos los músicos!

Webgrafía:

https://es.wikipedia.org/wiki/Escala_pentat%C3%B3nica

https://es.wikipedia.org/wiki/Potenciaci%C3%B3n

https://es.wikipedia.org/wiki/Logaritmo

https://en.wikipedia.org/wiki/Ut_queant_laxis

https://es.wikipedia.org/wiki/Pascal_%28unidad%29

https://es.wikipedia.org/wiki/Newton_%28unidad%29

http://www.asifunciona.com/tablas/intensidad_sonidos/intensidad_sonidos.htm

http://www.mentesenblanco-razonamientoabstracto.com/musica-origen-notas.html

Juan Francisco Martínez Cerdá

Investigador, Universitat Oberta de Catalunya (UOC)