“La música es el placer que experimenta la mente humana al contar sin darse cuenta de que está contando”, Gottfried Leibniz (1646-1716)
¿Qué tal? ¿Cómo va este inicio de año 2011? Espero que podamos seguir compartiendo a lo largo de este año algunas de las conexiones que se dan entre la música y las matemáticas.
Ya que acabamos de empezar un nuevo año, y que este hecho -que tiene que ver con la astronomía- es algo que se repite a lo largo del tiempo, como todos sabéis, podemos hablar del concepto de repetición de determinados sucesos. Por ejemplo, todos somos conscientes de que el día y la noche, las semanas, los meses, las estaciones o los años, son sucesos físicos que se repiten y que pueden ser medidos gracias a determinados instrumentos que el hombre ha ido investando, descubriendo, desarrollando, adaptando y perfeccionando desde el inicio de los tiempos. De alguna manera, para las medidas que el hombre ha ido realizando de todos aquellos sucesos que ha querido observar, y gracias a las matemáticas, se ha ido avanzando en la mejor métrica para dicha medición, en su simplificación y en su belleza: en su armonía, en última instancia. ¿Os suena alguno de estos conceptos: repetición, medida, armonía? Estoy seguro de que sí: cuando hacemos música, tenemos unas medidas (compases, notas, etc.), unas repeticiones (melodías, canons, etc.), y una armonía (relaciones entre sonidos simultáneas).
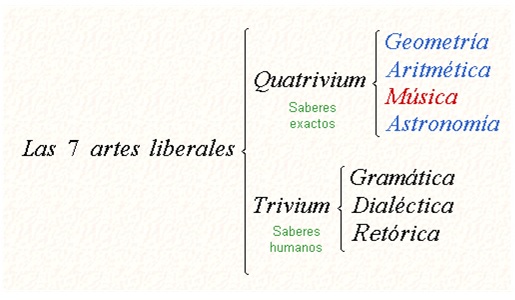
El origen del término “música” es la palabra griega “musiké” (“de las musas”), y aparecía como una de las siete artes liberales, asociada a los Saberes exactos (Quatrivium o Matemáticas):
Como podéis ver, antiguamente quien decidiese estudiar Matemáticas debía aprender también Música. En mi opinión, es una pena que hoy en día no ocurra así, y que sean disciplinas no comunes.
Respecto al concepto de repetición, que comentaba antes que puede aplicarse a melodías, ¿conocéis alguna de las oberturas de Rossini? La de “Guillermo Tell” o la de “El barbero de Sevilla” son absolutamente brillantes y, básicamente, formadas por repeticiones. Si hace tiempo que no las escucháis, probad a hacerlo bajo este punto de vita matemático.
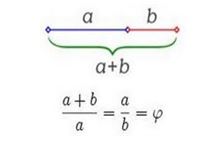
Si hablamos de medidas, quizás conozcáis la denominada “razón áurea”, que es aquel número obtenido de una figura geométrica en la que la proporción de alguna de sus partes C con respecto a su parte B inmediatamente mayor en tamaño, es igual a la proporción de esta parte mayor B con respecto a su superior C. Por ejemplo:
- La proporción entre la longitud del segmento a y el segmento b, es igual a la del segmento a+b y el segmento b:
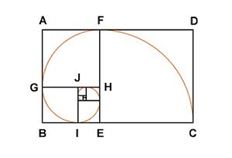
- La proporción entre el rectángulo ADCB y AFEB, dado por las proporciones entre AD y DC, y AB y AF:
Pues resulta que esta razón áurea la encontramos entre algunas de las partes de instrumentos como el violín:
Y no solamente eso. También encontramos que la razón áurea aparece en el primer movimiento de la Sonata Nº 1 de Mozart, que está dividido en 38 y 62 compases, y en su segundo movimiento, con 28 y 46 compases. Las proporciones entre ambos pares de números se corresponden con el número áureo. Incluso se puede encontrar otra aproximación a dicha razón en la Quinta Sinfonía de Beethoven, en la que su famoso lema parece en compases relacionados con dicho número:
Interesante, ¿verdad? Me pregunto si los compases de “Corazón yeclano” tienen también esta proporción, o si el repiqueteo que se oye cuando los pajes de las Fiestas de la Virgen guardan también dicha razón. ¡Qué lástima no tener aquí una partitura para comprobarlo! 🙂
Acabaré el artículo comentando algunos libros relacionados con nuestro tema, para que podáis ir creando una pequeña biblioteca sobre el tema:
- “El Armonógrafo”, de Anthony Ashton. Ediciones Orino. Colección: La aventura de la ciencia.
Este libro nos explica la relación entre las notas musicales y los números enteros, y nos presenta diversos gráficos generados por el armonógrafo, un instrumento inventado en el siglo XIX que genera dibujos mediante un péndulo, a partir de los sonidos que recibe.
- “La idea del cosmos. Cosmos y música en la antigüedad”, de Radamés Molina Montes y Daniel Ranz Riera. Ediciones Paidós Ibérica. Colección: Paidós studio.
Aquí se nos ofrece una visión de la historia del mundo a través de la interpretación en clave musical y matemáticas de algunos de los sucesos más importantes ocurridos, ya sea en el ámbito de la filosofía, la política, la medicina, la arquitectura, la teología o la técnica.
- “El número sonoro: La matemática en las teorías armónicas de Salinas y Zarlino”, de Amaya Sara García Pérez. Editorial: Caja Duero (Salamanca).
Esta publicación nos ilustra las diversas investigaciones de dos teóricos del siglo XVI, que analizaron las teorías existentes hasta la época, en materia de interrelación entre música y matemáticas. El libro nos presenta las diferentes relaciones históricas entre las entonaciones, la armonía y las proporciones existentes entre las notas musicales, desarrolladas y estudiadas a través de las matemáticas. Además, nos ofrece interesantes preguntas de carácter filosófico: ¿siempre tiene que ser percibida la música mediante el sentido del oído, además de por la razón, o podemos denominar música a cualquier estructura válida para la razón, como lo son las matemáticas?
Interesante cuestión, ésta última: ¿qué tiene que ser denominado “música”?
¿Lo sabemos? ¿Puede ésta ser definida de un modo colectivo, o la música siempre será algo subjetivo y personal?
¿Qué nos dice la razón?
¿Qué nos dice el corazón?
Mmmmmmnnnnnnnn…
¡Un saludo cordial!
Juanfran
———-
Juan Francisco Martínez Cerdá
Matemático, antiguo músico de la Banda de música de la Asociación de Amigos de la Música de Yecla.
Artículo aparecido en la Revista Diapasón de la Asociación de Amigos de la Música de Yecla.