¿Cuántos sonidos tiene una escala diatónica? ¿Cuántas líneas hay en un pentagrama?
Bueno… vamos a explicar algunos pequeños aspectos que tienen que ver con la música y las matemáticas.
¿Conocéis los números de Fibonacci? ¿No? Bueno, seguro que os habéis encontrado con ellos, aunque no os hayáis dado cuenta. La sucesión de Fibonacci es una serie formada por números que se relacionan entre ellos, bajo la regla de que cualquiera de los números es obtenido mediante la suma de los dos números anteriores. De este modo, empezando por los números 1 y 1, pues vamos obteniendo los diferentes elementos de dicha serie: 2 (=1+1), 3 (=1+2), 5 (=2+3), 8 (=3+5), 13 (=5+8), y, así, sucesivamente. La sucesión es, pues, la siguiente: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,… Es interesante también reseñar que la relación -o división- entre dos términos sucesivos tiende a aproximarse a la razón áurea, a medida que los números vayan incrementándose. ¿Recordáis que habíamos comentado en el anterior artículo en qué consistía la razón áurea? ¿Os acordáis que la habíamos relacionado con las distancias de un violín?
Os decía que puede que os hayáis encontrado con estos números, aunque sin daros cuenta, puesto que es normal que aparezca en diferentes situaciones de la naturaleza: la relación entre la altura de un ser humano y la altura de su ombligo, el tamaño de la espiral de la concha de los caracoles, el número de pipas en las diferentes las espirales de la flor de un girasol, la medida de las diferentes partes de los cuernos de algunos animales, la disposición de las hojas de la planta del aloe, etc.
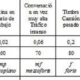
¿Por qué os hablo de la sucesión de Fibonacci? Pues porque ha sido utilizada por diferentes compositores. Uno de ellos es Béla Bartók (1881-1945), que desarrolló una escala músical, basándose en dicha sucesión numérica, y la llamó escala Fibonacci. La disposición de los tonos y semitonos se puede ver en la siguiente figura:
Este autor utiliza esta escala en el Tercer Movimiento de su obra “Música para instrumentos de cuerda, percusión y celesta”, en el que un xilófono abre con el ritmo siguiente: “1:1:2:3:5:8:5:3:2:1:1”. ¿Véis que son los primeros de la sucesión de Fibonacci?
En cuanto a su Primer Movimiento -también de esta obra-, Bartók elige a la fuga como forma musical para dicho movimiento, y utiliza un total de 89 compases: en los primeros 55 compases genera una tensión hasta un punto de clímax, y en los restantes 34 compases va disminuyendo poco a poco dicha sensación. ¿Qué tres números aparecen en este Primer Movimiento? 34, 55 y 89, todos ellos pertenecientes, como véis, a la sucesión de Fibonacci.
Otro compositor que podemos restacar aquí es Chopin (1810-1849), que también utiliza esta serie en su “Preludio en Sol menor”: basta sumar la duración de los compases que incluyen notas ligadas para obtener una pequeña sucesión de Fibonacci:
Un ejemplo de la relación entre la sucesión de Fibonacci y la música, que normalmente la tenemos delante de nosotros y ni nos enteramos, son las teclas de un piano. Seguro que las habéis mirando cientos de veces, pero nunca las habéis relacionado con la sucesión de Fibonacci. Echadle un ojo a la disposición de teclas que conforman una octava, y contad el número de teclas negras (2 por un lado, 3 por otro lado, esto es, 5 en total), el número de teclas blancas (8), y el número de teclas en total (13). ¿Véis que estos números pertenecen a la sucesión de Fibonacci: 2, 3, 5, 8, 13?
¿Interesante, verdad? Pues mirad ahora cómo se construye un intervalo de sexta mayor: a partir de la nota La, que sirve generalmente para afinar los instrumentos, podemos obtener un intervalo de sexta mayor mediante la combinación de la nota La y la nota Do, la primera obtenida mediante 440 vibraciones por segundo, y la segunda a través de 264 vibraciones por segundo: pues resulta que si dividimos 440/264 podemos llegar a la fracción 5/3, formada por el 5 y el 3, ambos números pertenecientes a la sucesión de Fibonacci.
¿Y qué pasaría con el intervalo de sexta menor? Haced la prueba, y veréis que también obtenéis otro par de números de esta sucesión.
Cambiemos ahora un poco de tema: seguro que todos habéis visto una trompeta. Imaginad que tuviéseis que pintarla, ¿creéis que podríais hacerlo? Sí, ¿verdad? ¿Y pensáis que podríais pintar cualquier tipo de trompeta?
Bueno, antes de que contestéis a esta pregunta, tengo que presentaros una trompeta matemática. Sí, una figura geométrica denominada Trompeta de Torricelli (o Trompeta de Gabriel), que resulta que es una figura que tiene un área infinita, pero encierra un volumen finito. Esta trompeta fue inventada por un estudiante de Galileo llamado Evangelista Torricelli (1608-1647). Su forma es obtenida mediante la rotación sobre el eje X de la siguiente función, siempre con valores de x mayores o iguales a 1:
Su forma en tres dimensiones es la siguiente:
Por sus características, es denominada Trompeta de Gabriel, en referencia a la trompeta -o cuerno- que hace sonar el arcángel Gabriel para anunciar el día del Juicio Final, ya que asocia el concepto de lo divino con lo terrenal: lo infinito con lo finito.
Como véis, tenemos una trompeta con área infinita y volumen finito, que no podríais pintar jamás, aunque sí llenarla de aire con vuestros pulmones. ¿Paradójico, verdad?
Bibliografía y Webgrafía:
Asociación Conocimiento Comunal – CONOMUN (2009). Matemáticas, música y algoritmia. Epistemowikia. Revista «Hiperenciclopédica» de Divulgación del Saber, nov 2009.
Livio, M. (2002). The Golden Ratio: The Story of Phi, The World’s Most Astonishing Number. New York: Broadway Books.
http://web.educastur.princast.es/ies/pravia/carpetas/profes/departam/mates/musica/index.htm
http://en.wikipedia.org/wiki/Fibonacci_numbers_in_popular_culture
http://solomonsmusic.net/diss7.htm
http://www.mi.sanu.ac.rs/vismath/jadrbookhtml/part42.html
http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibInArt.html#beet
Juan Francisco Martínez Cerdá
Investigador, Universitat Autònoma de Barcelona (UAB)